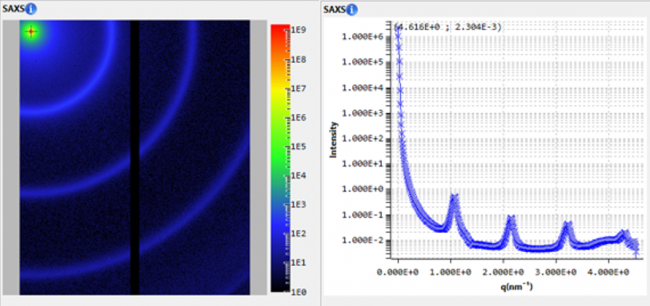
What are the advantages and limitations of small angle X-ray scattering (SAXS) and dynamic light scattering (DLS), and how do they complement each other?
Nanomaterials play a crucial role in modern society, revolutionizing industries and technologies across the board [1]. In medicine, nanoparticles (NPs) enable targeted drug delivery systems [2], precision medicine and advanced diagnostic tools [3, 4]. In electronics, nanomaterials such as graphene or carbon nanotubes enhance device performance, paving the way for faster and more efficient electronic devices. Moreover, nanomaterials hold promise in renewable energy technologies [5], catalysis [6], environmental sensing and water treatment, among other areas.
At the same time, their widespread use also raises concerns about potential environmental and health impacts, leading to the development of regulatory frameworks that ensure their safe and responsible application. However, establishing uniform definitions for nanomaterials has proven challenging due to their diverse compositions, structures and properties [7]. There is nonetheless consensus that nanomaterials are generally considered to be materials with features between 1 and 100 nanometers. Most definitions require thus that particles at the nanometer scale are identified and counted. As regulatory definitions specify quantifiable thresholds of the percentage of particles that must be at the nanometer scale, particle size determination with high accuracy becomes an essential step.
Various techniques are routinely employed to analyze the structure of materials at the nanometer scale. Scattering methods such as small angle X-ray scattering (SAXS) and dynamic light scattering (DLS) are well-established and commonly used in both academic and industrial settings. While they share some similarities, such as their ability to provide information about particle size and size distribution, they also have distinct advantages and limitations that make them complementary to each other. In this article, we will explore the potential of each technique and the benefits brought by employing a combination of the two.

Comparative description of SAXS and DLS
SAXS relies on X-ray scattering to probe the nanostructure of materials. When X-rays interact with the sample, they scatter in various directions based on electron density fluctuations within the material. This implies that objects should present a sufficiently high electronic contrast with the surrounding continuous phase [8]. By measuring the intensity of scattered X-rays at small angles, SAXS provides information about particle size, shape, internal structure and aggregation state. Moreover, it can reveal pore size and size distribution, as well as shape determination, along with structural information ranging from sub-nanometer to micrometer scale. This is achieved through various angular ranges (wide, small, and ultra-small angles WAXS/SAXS/USAXS) and geometries (transmission or grazing incidence GISAXS) on both bulk samples and surfaces.
DLS, on the other hand, measures fluctuations in scattered light intensity caused by the Brownian motion of particles in solution. A laser beam directed at the sample is scattered by the particles and recorded at a specific angle over time. The rate of intensity fluctuations in the scattered light is directly related to the diffusion coefficient of the particles, which in turn can be used to determine the hydrodynamic radius through the Stokes-Einstein relation [9]. Large particles diffuse more slowly and produce intensity fluctuations, while smaller particles diffuse more rapidly and produce faster fluctuations. By analyzing the autocorrelation function of the intensity fluctuations, DLS can provide information about the distribution of particle sizes in the sample, including the average particle size and the polydispersity of the sample. Relying on the Brownian motion of particles suspended in a fluid medium means that DLS is particularly suitable for analyzing nanoparticles, macromolecules, and other particles in solution, but it is not applicable to samples in other states such as solids or high-density gels.
Both SAXS and DLS are indirect techniques that require a physical model to extract the nanoparticle size from the raw experimental signal. DLS relies on the principle of Rayleigh scattering, which states that the intensity of light scattered by a particle is directly proportional to the sixth power of its diameter [10]. Thus, large-diameter NPs scatter light orders of magnitudes more intensively than smaller ones making DLS a technique with limited capabilities of resolving bimodal and heterogeneous ensembles of particles. Moreover, DLS may not accurately represent particles with non-spherical or irregular shapes, as it simplifies their geometry to that of spherical non-interacting particles for analysis employing the Stokes-Einstein equation.
One such example is the following morphological analysis of bimodal silica nanoparticles. As shown in Figure 1, DLS measurements yielded a unimodal particle size distribution even though the evaluation method for the autocorrelation function is capable of describing multimodal distributions [10]. On the other hand, SAXS was able to resolve the size and ratio of the two populations providing thus a statistically relevant description of the bimodal silica nanoparticles system.
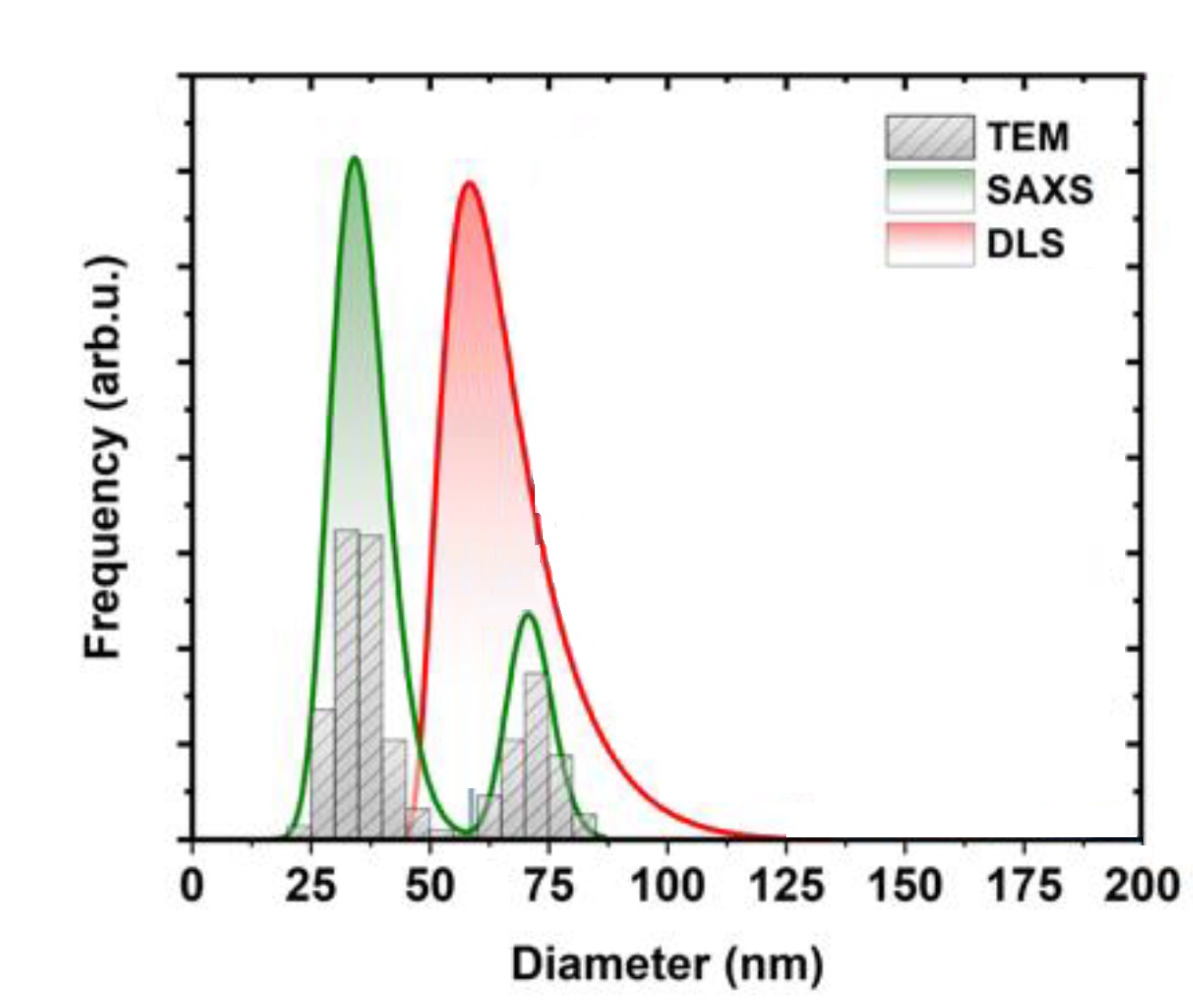
Fig. 1 Particle size distribution of bimodal silica nanoparticles as determined by SAXS, DLS and Transmission electron microscopy (TEM). Credit: Materials, 2020, DOI: 10.3390/ma13143101.
Besides the heterogeneity of the sample, other aspects such as particle shape and porosity can greatly influence the results. It is therefore advisable to pay careful consideration when interpreting numerical values of the size of nanoparticles from different methods [11]. Thus, employing multiple measurement methods rather than relying solely on a single technique is advantageous to obtain an accurate view of the size, size distribution and shape of nanoparticles.
Combined SAXS and DLS analysis reveals the impact of hydrophilic block length on spherical nano-objects
Polymerization-induced self-assembly (PISA) is an established method for preparing block copolymer nano-objects with tailorable sizes and morphologies such as spheres, worms, or vesicles. These find applications in various fields such as food, cosmetics, or pharmaceuticals.
PISA is typically conducted by reversible addition fragmentation chain transfer (RAFT) polymerization of a soluble monomer in the presence of a soluble macromolecular chain transfer agent (macro-CTA). A group of researchers from the University of Leeds and Diamond Light Source used SAXS in combination with DLS to characterize the formation and morphological evolution of spherical block copolymer nano-objects during RAFT polymerization of diacetone acrylamide in the presence of a series of poly(dimethylacrylamide) (PDMAm) macromolecular chain transfer agents with varying degrees of polymerization (DP) [12].
DLS was used to determine hydrodynamic diameter (Dh) as well as the polydispersity index (PDI) via the Stokes–Einstein equation assuming spherical and independent particles. SAXS on the other hand enabled the determination of the core diameter (Dcore) amongst other structural parameters such as the aggregation number, the radius of gyration of individual corona chains and the volume fraction of solvent and unreacted monomer within the core.
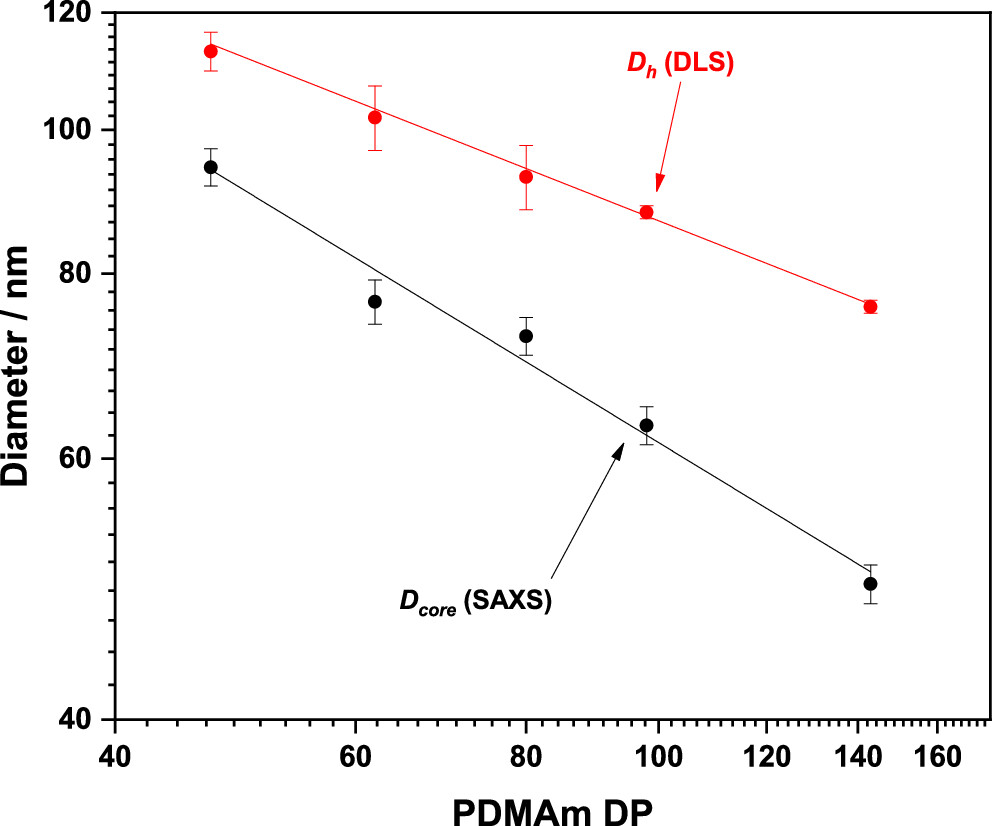
By comparing Dh and Dcore measurements, researchers were able to understand how the corona (the outer layer of the particle) contributes to the overall size and structure of the particle. Figure 2 shows that both the hydrodynamic and the core diameters decrease as a function of increasing the degree of polymerization (DP) of PDMAm. However, the different rates at which the two decrease indicate that the thickness of the apparent corona increases.
Fig. 2 Evolution of core diameter (Dcore), determined by SAXS, and Hydrodynamic diameter (Dh), determined by DLS, as a function of PDMAm macromolecular chain transfer agents with varying degrees of polymerization (DP). Credit: Macromolecules, 2023, DOI: 10.1021/acs.macromol.3c00585.
As shown in Figure 3, using a combination of SAXS and DLS analysis, researchers proved that despite the reduced overall diameter of the particles as a function of increasing DP of PDMAm, the contribution of the corona itself is increasing. This information would not have been attainable by employing only one of the two techniques.
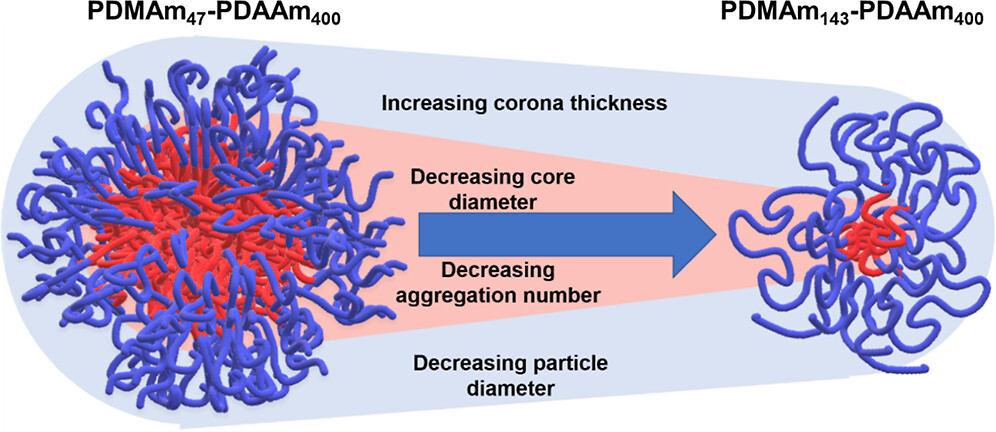
Fig. 3 Schematic representation of the variation in particle dimensions as the degree of polymerization (DP) of the PDMAm macro-CTA increases from 47 to 143, while the PDAAm core DP remains approximately 400. Credit: Macromolecules, 2023, DOI: 10.1021/acs.macromol.3c00585.
Conclusions
In summary, routine particle size characterization methods such as dynamic light scattering can benefit greatly from the use of orthogonal techniques such as small angle X-ray scattering. While DLS offers cost-effective and straightforward size analysis, its limitations become apparent when dealing with complex particle distributions, often providing a simplified representation (e.g assumption of spherical particle geometry).
SAXS, instead, offers higher resolution and the capability to discern multiple particle populations accurately. Moreover, SAXS is sensitive to particle shape and internal structure, offering detailed information about particle morphology. SAXS also provides more versatility for analyzing particles in various states (gel, solid, powder, liquid) whereas DLS is limited to particles in solution. Additionally, in contrast with SAXS, DLS is highly sensitive to sample concentration. At higher concentrations, particles tend to interact more strongly, leading to increased multiple scattering effects. This can result in distorted data and inaccurate particle size measurements. To mitigate these effects, DLS typically requires samples to be highly diluted, often to dilution factors of 1/1000 or even lower. This extensive dilution process can be time-consuming and may not be feasible for samples with limited availability or stability.
As demonstrated in this article, there are instances where neither technique alone can provide a comprehensive understanding of the sample. Combining DLS with SAXS not only overcomes the limitations inherent in each method but also bridges the gap between partial insights and a thorough characterization of the particle system.
| SAXS/WAXS/GISAXS/GIWAXS | DLS | |
| Types of samples | gel, solid, powder, liquid (turbid or not) | dilute solutions |
| Sample preparation | Minimal | Moderate |
| Observation volume | 0.1 – 1 mm³ | 0.001 - 1 mm³ |
| Range | < 1 - 350 nm (up to 1.5 µm USAXS) | 0.15 nm – 10 µm |
| In-situ or operando | Yes | Yes |
| Measuring time | Fast | Fast |
| Statistics | Statistically relevant results | Statistically relevant results |
| Spatial Resolution | Low | Low |
| Data | Scattering pattern in reciprocal space | Intensity fluctuations of scattered light as a function of time |
| Data interpretation | Requires data fitting expertise | Requires careful interpretation of the results |
| Beam damage | No | No |
| Limitations | Requires sufficient electron density contrast | Biased towards larger particles, requires samples optically transparent to the laser wavelength |
| Information | Size, shape, crystallinity, orientation, bulk surface nanostructures, correlation function, crystalline and nanostructure phases identification | Particle size and size distribution, diffusion coefficients and aggregation kinetics |
[1] S. Malik, K. Muhammad, and Y. Waheed, Nanotechnology: A Revolution in Modern Industry, Molecules 28, 661 (2023). DOI: 10.3390/molecules28020661.
[2] M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas, et al., Engineering Precision Nanoparticles for Drug Delivery, Nat Rev Drug Discov 20, 101 (2021). DOI: 10.1038/s41573-020-0090-8.
[3] K. W. Cho, S.-H. Sunwoo, Y. J. Hong, J. H. Koo, J. H. Kim, et al., Soft Bioelectronics Based on Nanomaterials, Chem. Rev. 122, 5068 (2022). DOI: 10.1021/acs.chemrev.1c00531.
[4] J. Damodharan, Nanomaterials in Medicine – An Overview, Materials Today: Proceedings 37, 383 (2021). DOI: 10.1016/j.matpr.2020.05.380.
[5] A. A. İnada, S. Arman, and B. Safaei, A Novel Review on the Efficiency of Nanomaterials for Solar Energy Storage Systems, Journal of Energy Storage 55, 105661 (2022). DOI:1016/j.est.2022.10566.
[6] P. Gómez-López, A. Puente-Santiago, A. Castro-Beltrán, L. A. Santos do Nascimento, A. M. Balu, et al., Nanomaterials and Catalysis for Green Chemistry, Current Opinion in Green and Sustainable Chemistry 24, 48 (2020). DOI: 10.1016/j.cogsc.2020.03.00.
[7] K. Rasmussen, J. Riego Sintes, and H. Rauscher, How Nanoparticles Are Counted in Global Regulatory Nanomaterial Definitions, Nat. Nanotechnol. 19, 132–138 (2024). DOI: 10.1038/s41565-023-01578-x.
[8] J.-M. Teulon, C. Godon, L. Chantalat, C. Moriscot, J. Cambedouzou, et al., On the Operational Aspects of Measuring Nanoparticle Sizes, Nanomaterials 9, 18 (2019). DOI: 10.3390/nano9010018.
[9] R. Pecora, Dynamic Light Scattering Measurement of Nanometer Particles in Liquids, Journal of Nanoparticle Research 2, 123 (2000). DOI: 10.1023/A:1010067107182.
[10] M. A. Al-Khafaji, A. Gaál, A. Wacha, A. Bóta, and Z. Varga, Particle Size Distribution of Bimodal Silica Nanoparticles: A Comparison of Different Measurement Techniques, Materials 13, 14 (2020). DOI: 10.3390/ma13143101.
[11] R. F. Domingos, M. A. Baalousha, Y. Ju-Nam, M. M. Reid, N. Tufenkji, et al., Characterizing Manufactured Nanoparticles in the Environment: Multimethod Determination of Particle Sizes, Environ. Sci. Technol. 43, 7277 (2009). DOI: 10.1021/es900249m
[12] J. D. Guild, S. T. Knox, S. B. Burholt, Eleanor. M. Hilton, et al., Continuous-Flow Laboratory SAXS for In Situ Determination of the Impact of Hydrophilic Block Length on Spherical Nano-Object Formation during Polymerization-Induced Self-Assembly, Macromolecules 56, 6426 (2023). DOI: 10.1021/acs.macromol.3c00585.
Products
Discover our SAXS instruments in the lab
Xeuss Pro
The Ultimate Solution for Nanoscale Characterization using SAXS/WAXS/GISAXS/USAXS/Imaging